Minute of Angle
Most firearm sighting scopes incorporate windage and elevation adjustments referenced to MOA (minute of angle). Each click of the scope turret is usually 1/4 MOA change and on some scopes 1/8 MOA. Normally, shooters refer to these adjustments as a change of a fraction of an inch at 100 yards rather than the true value of MOA for which they are supposedly calibrated to. The value of inch is a nice easy number to work with and most of us can easily visualize its length and its multiples without the aid of a calculator. Actually the comparison is close enough to not be of practical concern, especially at distances up to a few hundred yards, and the real difference is a mere 0.47 inch at 1000 yards. For serious target shooting and as shooting distances increase the attention to MOA value relative to sight adjustment becomes more essential.
Calculating Minute of Angle
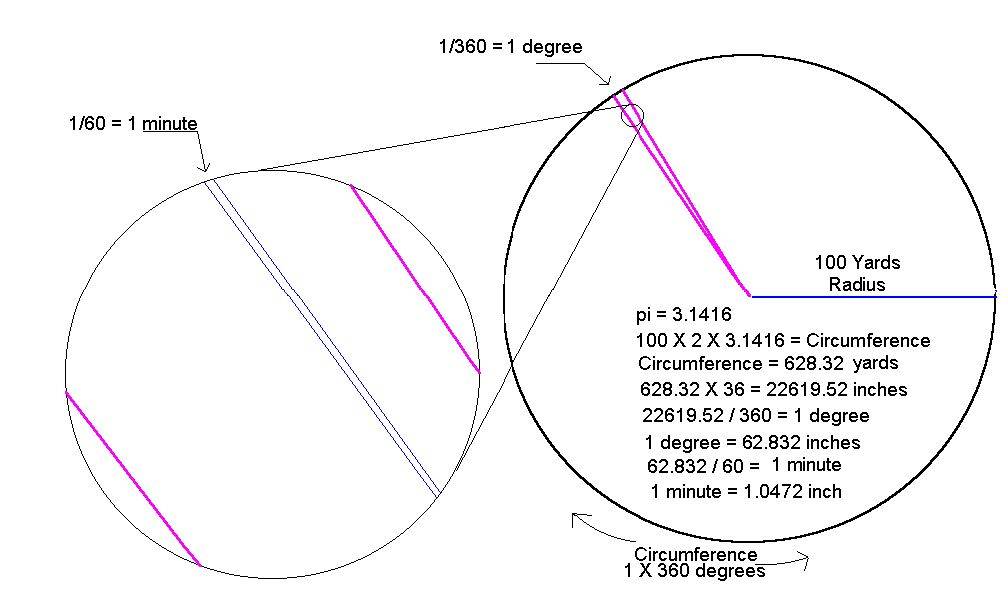
The angle of an arc is expressed in number of degrees. There are 360 degrees of arc to a full circle. Each degree consists of 60 minutes of arc. The distance covered by the measure of arc is relative to the circumference (total distance around the circle) it is contained within. Knowing the radius (distance to center of circle) circumference is easily calculated by using the constant pi . The ratio (represented by pi ) of circumference is constant to diameter (radius x 2) regardless of circle size. The precise value of pi is so far unknown to man but is normally resolved to 3.1416 or 3.141 for our purposes.
- Suppose a circle with a 6 inch radius. Circumference can be calculated as:
circumference = (radius x 2) x pi
circumference = (6 x 2) x 3.1416
circumference = 12 x 3.1416
circumference = 37.6992 inches
The distance covered by 1 degree of angle (37.6992 / 360 or, circumference divided by 360 degrees) is 0.1047 inch at 6 inches from center of circle.
And, 1 minute of angle represents (0.1047 / 60 or, 1 degree divided by 60 minutes) 0.001745 inch at 6 inches from center of circle.
Knowing what MOA represents allows us to calculate its value to any distance.
Six inches (the radius of the above example) is 1/600th of 100 yards: (100 yards x 36 inches) / 6 inches = 600
Therefore, the value of MOA at 100 yards is 1.047 inches (0.001745 x 600 = 1.047)
At 50 yards 1/2 the 100 yard value; 70% @ 70 yards; twice @ 200 yards; 6 times @ 600 yards; and so on.
So, the difference between thinking in inches as opposed to MOA is 0.47 inch @ 1000 yards.
Four (4) clicks of the scope adjustment equals 1.047 inch change @ 100 yards for scopes of 1/4MOA per click.
Where group size is expressed in inches the word 'inch' should be spelled. Writing the symbol commonly used to represent the measure of inch (") is not accurate here, and in fact misleading since that symbol also represents 'second of angle' (1/60 of a minute of angle). Therefore, a group of 1 inch would properly be written as '1 inch' not 1". It could also be written as 1' since that symbol (') is used to represent minute of angle but that might be misleading to those thinking in feet.
Why Use MOA
As shown above, the value of a measure of angle can easily be calculated to any distance from its source of origin - center of circle or muzzle of barrel. Such measures as MOA (minute of angle) are also part of our only universal language - mathematics. While knowing a rifle has a precision of a certain value of the inch at a particular distance also makes it simple to calculate its precision at other distances, one would have to know both the distance and the measure in inch (example: 1 inch @ 100 yards) before calculating it to other distances. In contrast, knowing only the measure of angle is needed to do the same. An example of the contrast is expressing 0.73 inch @ 100 yards verses 0.7 MOA (0.73 / 1.0472 = 0.697). The two equate practically the same (1 MOA = 1.047 inch @ 100 yards) but the expression using MOA is more concise since no distances are included in the expression.
Two informative sites for further discussion of MOA relative to firearm use: What Is MOA and Is It Really an Inch At 100 Yards? and Mil-dots and Minutes-of-angle, From a Technical Perspective
Calculating Scope Click
For long ranges where shooting distances may vary considerably it is wise to know the actual value of each scope adjustment. This is especially true if scope settings are changed in the field as shooting distances change. Not all scopes are precisely calibrated to MOA (minute of angle) or to the inch. Below is a procedure learned from Varmint Al's Shooting Page for better determining the value of each click of the scope turret.
Shooting from a solid bench rest, determine the center of group using the Average Group Radius method. Without reaching the adjustment limit of the scope, make and record as many scope elevation clicks as will still keep the group on the target while shooting at the same aiming point as before. Again determine center of group using the Average Group Radius method. Return the scope elevation to its previous setting. Determine the distance between the center of the two groups. Divide that distance by the number of elevation clicks used to achieve group two. That is the calculated value of change for that distance for each click.
For high power rifles it is recommended the target be no less than 100 yards distance as some projectiles may not completely stabilize at shorter distances, thereby giving a false indication of true performance.
----->Go to Next Page (Calculating Rifle Precision)
<-----Go back to Previous Page
Other Topics available:
Wood Stains and Gun Stocks
Floating the Barrel
Glass Bedding
Pillar Bedding
Barrel Bedding Block
Inlays, Tips, and Caps
What is M.O.A.?
Calculating Rifle Precision
Target Crowning a Muzzle
Building a Muzzle Loader from Kit
Eliminate Trigger Over-Travel
Attaching the Recoil Pad